С учетом экспоненциального роста объемов аудиовизуальной информации, становится все актуальнее вопрос о поиске методов эффективного преобразования и сжатия этой информации. Один из методов преобразования разработал еще 200 лет назад математик Жан Батист Жозеф Фурье.
В чем суть метода Фурье для сжатия информации?
Существует большое число технологий и математических методов для сжатия изображений. Однако каким бы ни был алгоритм, используемый для сжатия информации (далее будем делать практический разбор на примере сжатия изображений, это наиболее наглядно и просто для восприятия), принцип алгоритма всегда будет заключаться в следующем: найти и описать закономерности в массиве информации.
Итак, алгоритмы сжатия сводятся к поиску закономерностей в массиве данных. И чем больше удастся выявить закономерностей, тем больше будет избыточности, и тем меньший объем информации останется после сжатия.
Можем легко увидеть это на простейшем примере. Откроем любую программу для рисования изображений (например, стандартный Paint). И закрасим всю область одним единственным цветом. Сохраним изображение. Размер изображения — 1.28 Кб

Теперь создадим изображение такого же размера в той же программе, но и использованием разных цветовых палитр и композиций. Размер изображения сразу увеличивается до 9 Кб.

Это наглядный пример работы методов сжатия изображений. В данном случае кодировщик разглядел закономерность в том, что все пиксели первого изображения имеют одинаковую яркость и цвет, поэтому изображение получилось в несколько раз “легче” второго, где таких закономерностей меньше. Простой пример, показывающий важность использования методов сжатия информации. В частности, в формате JPEG для сжатия используется именно метод Фурье.
Теория относительности — Гений Эйнштейна
Фурье начал разработку своего метода еще в конце 18 века. Метод Фурье — это один из самых распространенных методов решения уравнений с частными производными, показывающий высокую практическую и теоретическую эффективность. Сам метод часто можно встретить под другими названиями: метод разделения переменных либо метод собственных функций.
Основной базой для сжатия информации является представление функций тригонометрическими рядами Фурье. Сами ряды Фурье являются способом представления произвольной сложной функции путем суммирования нескольких простых функций.
Как это работает на практике на примере аппроксимации изображений?
Аппроксимация — это научный подход замены одних объектов в массиве данных другими. Конечным результатом аппроксимации может быть в том числе и сжатие данных, которое нас интересует.
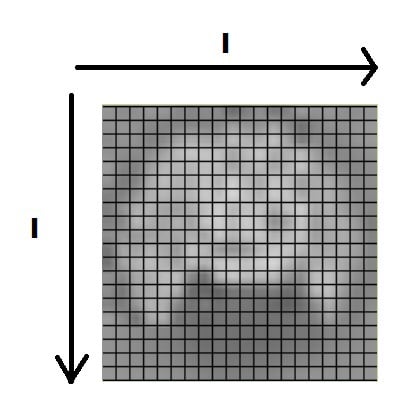
Давайте представим монохромное (черно-белое изображение) размером l на l пикселей в виде сеточной функции ƒ(i, j), где:
- i, j — координаты конкретного пикселя нашего монохромного изображения;
- i, j могут принимать значение от 1 до l (количество пикселей по одной стороне в нашем изображении).
Значением функции является яркость конкретного пикселя. Значение яркости меняется от 0 до 255. В процессе сжатия монохромного изображения функция яркости будет подвержена аппроксимации частичной суммы дискретного разложения по косинусам.
На первом этапе в процессе сжатия изображения используются дискретные аналоги рядов Фурье.
На втором этапе уже аппроксимированное изображение проходит этап квантования — это процесс деления непрерывного динамического диапазона значений яркости на ряд дискретных уровней при цифровой обработке изображения.
Ошибка выжившего — парадоксально, но факт!
Третьим этапом является группировка данных.
Четвертый и последний этап сжатия — архивирование. Именно по этому принципу работает, например, технология JPEG.
Практическая реализация. Прикладное применение метода
Использование метода Фурье получило широкое практическое применение, и используется программистами и разработчиками для:
- Сжатия изображений;
- Сжатия видео;
- Сжатия аудио;
- Оперирования большими объемами данных;
- Прогнозирования событий (в частности для аппроксимации временных рядов);
- Обучение нейронных сетей, искусственного интеллекта, data science.
На сегодняшний день используются 3 подхода для практического использования метода Фурье. Рассмотрим их также на примере работы с изображением.
Подход первый. Этот подход мы уже рассмотрели в примере ранее. Его суть заключается в аппроксимации изображения как сеточной функции с двумя переменными. Для применения подхода необходим дискретный аналог кратного ряда Фурье. Этот способ не нашел широкого и повсеместного практического применения, поскольку подразумевает использования больших количеств машинных ресурсов и времени.
Подход второй. Суть подхода состоит в разбиении изображения на отдельные строки пикселей, после чего происходит отдельная аппроксимация каждой конкретной строки.
Этот подход в практическом смысле значительно эффективнее предыдущего, потому что здесь обрабатываются функции одной переменной, а не двух.
Великий аттрактор — то, что притягивает Землю с огромной силой!
Подход третий. Суть подхода заключается в разбиении изображений на отдельные прямоугольные блоки, после чего осуществляется последовательная аппроксимация каждого блока по-отдельности.
Такой подход позволяет лучше всего бороться с эффектом Гиббса (ситуацией, когда изображение становится слишком “шумным”).
Пример реализации метода Фурье для сжатия изображений
В качестве примера реализации на практике метода Фурье рассмотрим монохромное изображение. На первом рисунке представлено исходное изображение. На втором после аппроксимации было сохранено ⅔ значений из массива данных изображения. На третьем изображении было сохранено ⅓ значений из массива данных изображения. Как вы можете видеть, качество изображения в третьем случае заметно ухудшилось, это и есть эффект Гиббса, о котором говорилось ранее.
Однако обратите внимание, что во втором случае изображение после сжатия сохранило качество и четкость, видны плавные переходы пикселей, а это означает, что при должном подходе метод Фурье отлично справляется со своими задачами.

Выводы
Исходя из полученной информации и изучения практических аспектов его применения, можно сделать вывод, что метод Фурье и за две сотни лет не утратил своей актуальности. А эффективность метода подтверждается его широким и повсеместным использованием для сжатия больших объемов информации, будь то аудиовизуальная информация или большие массивы данных.